神经网络初步

发表于 分类于

1. 损失函数的定义

根据 Y 类型的不同（数值型、类别型、顺序型），一般有三种损失函数：

  1. Regression loss functions，如 GDP 的预测问题
  2. Classification loss functions，如区分图片是猫还是狗
  3. ‍Ranking loss functions，如广告素材的排序问题

本文主要讨论分类问题（classification）的公式推导以及 R 代码示例的实现。

2. 分类问题和交叉熵

交叉熵 Cross entropy loss 是机器学习中常用的衡量分类模型表现如何的指标，熵是由 Claude Shannon 在 1948 年第一次引入。

\[ \begin{equation*} H(X) = -\Sigma_i P(X=i) \log _2 P(X=i) \end{equation*} \]

交叉熵 Cross-entropy 还经常被用于衡量两个概率分布之间的差异。假设有三个类别，标签为 A、B、C，他们的事实分布概率是：

Pr(A) Pr(B) Pr(C)
0.0 1.0 0.0

通过训练的某个机器学习分类器，预测的概率分布如下：

Pr(A) Pr(B) Pr(C)
0.228 0.619 0.153

我们显然希望预测分布 predicted distribution 同实际分布 true distribution 无限接近于 0，那这两个分布之间的差异有多大呢？是否在改善？这时候使用的就是交叉熵来度量的，公式如下：

根据公式计算两个分部之间的差异为：

1
2
3
4
5
d_true <- c(0, 1, 0)
d_predicted <- c(0.228, 0.619, 0.153)
H = -sum(d_true * log(d_predicted))
H
# [1] 0.47965

目测如果预测改善会出现什么情况：

1
2
3
d_predicted <- c(0.08, 0.81, 0.11)
-sum(d_true * log(d_predicted))
# [1] 0.210721

交叉熵变的更小了。假如我们认定预测值大于 0.5 即为 1 的话（传统的分类错误率），会发现这两组的预测精度是一样的（正确率都是 100%），显然无法更好的衡量模型的预测精度。

2.1. 二分类交叉熵

在将问题具象化到二分类问题，交叉熵的损失函数形式为：

\[ \begin{equation*} L = -(y \log(p) + (1-y) \log (1-p)) \end{equation*} \]

其中，\(y\) 是真实标签（0 或 1），\(p\) 是模型的预测概率（0 到 1 之间，比如通过 sigmoid 变换的结果）。

通过前面的示例演示以及数学性质，这个损失函数具有两条基本属性：

  1. 非负性
  2. 预测目标值越接近实际目标值时，损失函数接越近于 0

2.2. 拟合梯度下降

已知 sigmod 这个变换可以将线性预测的结果压缩到 0 至 1 之间，刚好表征了 0-1 类别的概率

\[ p = \sigma(s)=\frac{1}{1+e^{-s}}=\frac{e}{1+e^{s}} \]

\(s\) 为 \(x_i\) 的线性组合关系：

\[ s = \sum w_i x_i \]

我们希望损失函数（交叉熵）最小化，对系数 \(w_i\) 求导：

\[ \frac{\partial L}{\partial w_{i}}=\frac{\partial L}{\partial p} \frac{\partial p}{\partial s} \frac{\partial s}{\partial w_{i}} \]

这三项分别计算，可以得到以下结果。推导背景知识可以参考导数推导词条：

\[ \begin{align} \frac{\partial L}{\partial p} &= -y / p+(1-y) /(1-p) \\ \frac{\partial p}{\partial s} &= e^{s} /\left(1+e^{s}\right) * 1 /\left(1+e^{s}\right)=\sigma(s) *(1-\sigma(s)) \\ \frac{\partial s}{\partial w_{i}} &= x_{i} \\ \end{align} \]

有了上面推导结果，就可以利用梯度更新的方式求解 \(w_i\)：

\[ \begin{equation*} w_i \leftarrow w_i-\alpha \frac{\partial}{\partial w_i} L(w) \end{equation*} \]

用一个小例子（逻辑回归），来说明 \(w_i\) 更新的过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# input dataset
X <- as.matrix(iris[iris$Species != 'versicolor', 1:4])
# output dataset  
y <- c(rep(0, 50), rep(1, 50))

# sigmoid function
nonlin <- function(x, deriv = FALSE) {
	if(deriv == TRUE) x * (1 - x)
	else 1/(1 + exp(-x))
}

set.seed(1)

# initialize weights randomly with mean 0
w <- rnorm(4, 0, 0.1)
tmp <- list() # 记录w的变化
for (i in 1:100){
	l0 <- X
	l1 <- nonlin(l0 %*% w)
	l1_delta <- (y - l1) * nonlin(l1, deriv = TRUE)
  # update weights
  w <- w + 0.01 * t(l0) %*% l1_delta
  tmp[[i]] <- w
}
l1
table(l1 > 0.5, y)

## Coef's solution path
ts.plot(t(do.call(cbind, tmp)))

可以观察 coefficient path 的变化：

exp

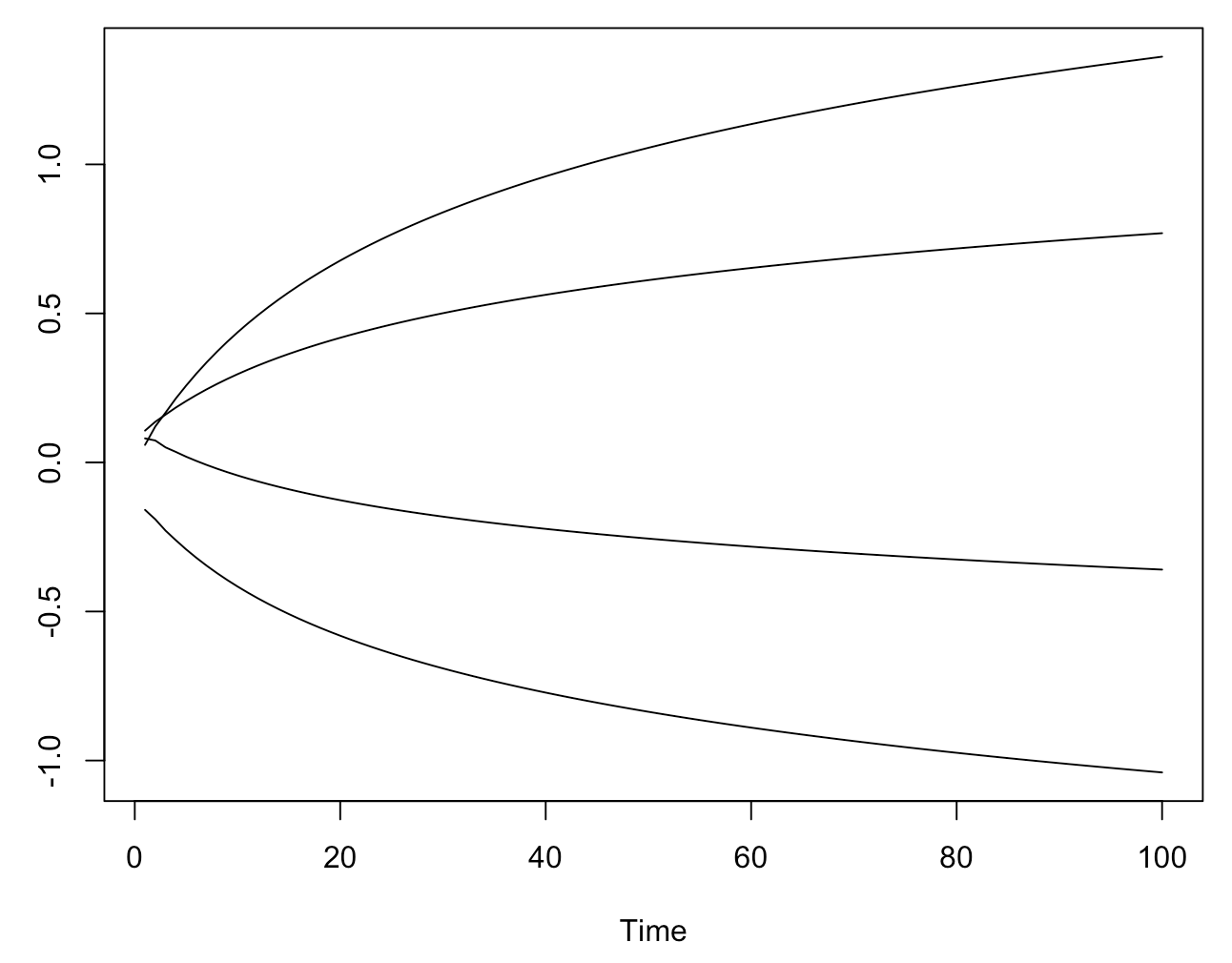
不过更为通泛的做法是将三者相乘，直接求得 \(\frac{\partial L}{\partial w_{i}}\) 的表达

\[ \begin{align} \frac{\partial L}{\partial w_{i}} &= [-y / p + (1-y) /(1-p)] * \sigma(s) *(1-\sigma(s)) * x_{i} \\ &= [-y / \sigma(s)+(1-y) /(1-\sigma(s))] * \sigma(s) *(1-\sigma(s)) * x_{i} \\ &= [-y * (1-\sigma(s))+(1-y) * \sigma(s)] * x_{i} \\ &= [\sigma(s)-y] * x_{i} \end{align} \]

我们得到了一个比前面推导更加漂亮的结果。将前面的例子重写一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# input dataset
X <- as.matrix(iris[iris$Species != 'versicolor', 1:4])
# output dataset  
y <- c(rep(0, 50), rep(1, 50))

sigmoid <- function(x){
    1/(1 + exp(-x))
}

w <- rnorm(4, 0, 0.1)
tmp <- list() # 记录w的变化
for (i in 1:100){
	l0 <- X
	l1 <- sigmoid(l0 %*% w)
  # update weights
  w <- w + 0.001 * t(l0) %*% (y - l1)
  tmp[[i]] <- w
}
l1
table(l1 > 0.5, y)

## Coef's solution path
ts.plot(t(do.call(cbind, tmp)))

3. 为什么不用 MSE

从前文可以看到，交叉熵权重学习的速率受到 \(\sigma(s) - y\) 的影响，也就是输出误差的控制，这样在误差较大时有更大的学习速度。再比较一下平方损失代价函数的学习速率，定义 Loss 为：

\[ L=\frac{1}{2}\left(p-y)^{2}\right. \]

且

\[ p = \sigma(s)=\frac{1}{1+e^{-s}}=\frac{e^{s}}{1+e^{s}} \]

则对其求偏导有

\[ (p-y) * \sigma(s) *(1-\sigma(s)) * x_{i} \]

不难看出，其偏导值在输出概率值接近0或者1的时候都会非常小，这可能会造成模型刚开始训练时，偏导值几乎消失。 这也是为什么我们不会使用 MSE 作为 0-1 回归 loss 的原因。

4. 标准神经网络

构建包含一个隐藏层 hidden layer 的神经网络，隐藏层有两个 cell。

1
2
3
4
5
6
7
8
9
10
11
library(visNetwork)
color.background <- c("red","red","red","red","blue","blue","green")
nodes <- data.frame(id = c(1,2,3,4,5,6,7), 
                    color.background = color.background,
                    label = c('I1', 'I2', 'I3', 'I4', 'H1', 'H2', 'O1'))
edges <- data.frame(from = c(1,2,3,4,1,2,3,4,5,6), 
                      to = c(5,5,5,5,6,6,6,6,7,7),
                    label = c(rep('', 10)))
visNetwork(nodes, edges, width = "100%") |>
  visEdges(arrows = "to") |>
  visHierarchicalLayout(sortMethod = 'directed')

exp

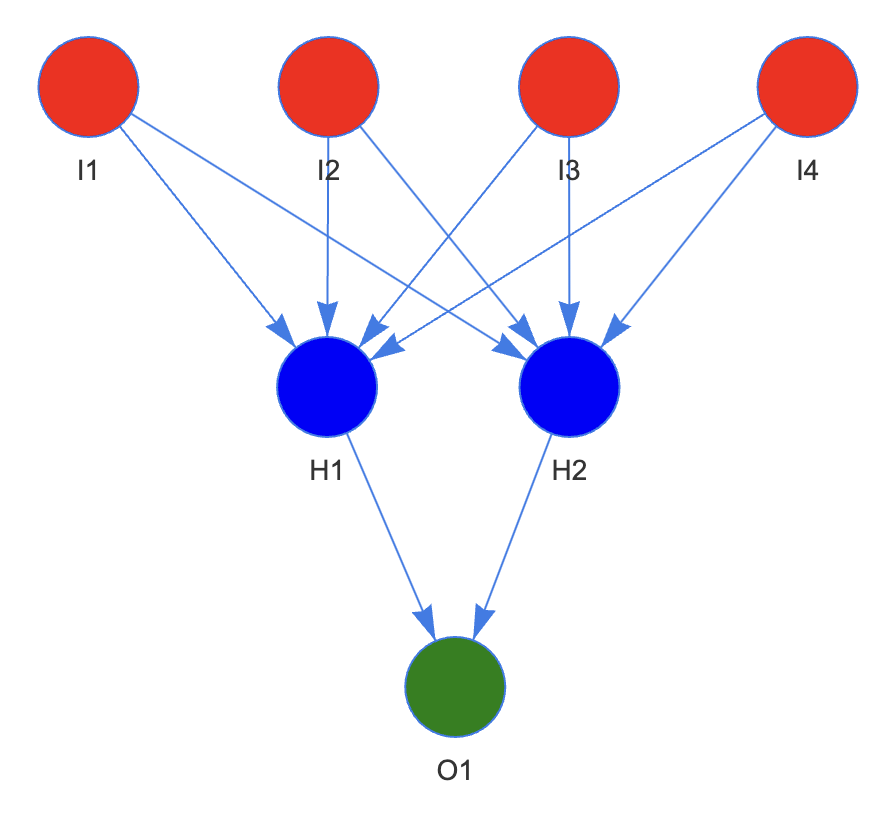
看看每个层的参数是如何更新的，两个关键映射

  • 4 个变量向 2 个 cell 的 sigmoid 映射
  • 2 个 cell 向 y 的 sigmoid 映射

对应的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
## include hidden layer
## input dataset
X <- as.matrix(iris[iris$Species != 'versicolor', 1:4])
# output dataset  
y <- c(rep(0, 50), rep(1, 50))

# sigmoid function
nonlin <- function(x, deriv = FALSE) {
	if(deriv == TRUE) x * (1 - x)
	else 1/(1 + exp(-x))
}

set.seed(1)

m <- ncol(X)
n <- 2 # number of cells of hidden layer
syn0 = matrix(rnorm(m*n, 0, 0.1), nrow = m, ncol = n)
syn1 = rnorm(n, 0, 0.1)

iter <- 500

M <- matrix(0, iter * 3, 3) # 测试scale后的效果和中值后的
M[,1] <- rep(1:iter, 3)
M[,3] <- rep(1:3, each = iter) # 三组实验

for(j in 1:iter){
	l0 <- X
	l1 <- nonlin(l0 %*% syn0)
	l2 <- nonlin(l1 %*% syn1)
	l2_delta = (y - l2) * nonlin(l2, deriv = TRUE)
	l1_error = l2_delta %*% t(syn1) # how much did each l1 value contribute to the l2 error (according to the weights)?
	l1_delta = l1_error * nonlin(l1, deriv = TRUE)
	## update weights
  syn1 <- syn1 + 0.01 * t(l1) %*% l2_delta
  syn0 <- syn0 + 0.01 * t(l0) %*% l1_delta
  M[j,2] <- sd(y - l2)
}

pred <- X %*% syn0 %*% syn1 |> nonlin()
table(pred > 0.5, y)

能不能加快迭代速度？显然是可能的，有两个思路：

  1. 标准化
  2. 中心化

我们看看这两个思路的效果如何？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
m <- ncol(X)
n <- 2 # number of cells of hidden layer
syn0 = matrix(rnorm(m*n, 0, 0.1), nrow = m, ncol = n)
syn1 = rnorm(n, 0, 0.1)

for(j in 1:iter){
	l0 <- scale(X)
	l1 <- nonlin(l0 %*% syn0)
	l2 <- nonlin(l1 %*% syn1)
	l2_delta = (y - l2) * nonlin(l2, deriv = TRUE)
	l1_error = l2_delta %*% t(syn1) # how much did each l1 value contribute to the l2 error (according to the weights)?
	l1_delta = l1_error * nonlin(l1, deriv = TRUE)
	## update weights
  syn1 <- syn1 + 0.01 * t(l1) %*% l2_delta
  syn0 <- syn0 + 0.01 * t(l0) %*% l1_delta
  M[j + iter,2] <- sd(y - l2)
}


m <- ncol(X)
n <- 2 # number of cells of hidden layer
syn0 = matrix(rnorm(m*n, 0, 0.1), nrow = m, ncol = n)
syn1 = rnorm(n, 0, 0.1)

for(j in 1:iter){
	l0 <- t(t(X) - colMeans(X))
	l1 <- nonlin(l0 %*% syn0)
	l2 <- nonlin(l1 %*% syn1)
	l2_delta = (y - l2) * nonlin(l2, deriv = TRUE)
	l1_error = l2_delta %*% t(syn1) # how much did each l1 value contribute to the l2 error (according to the weights)?
	l1_delta = l1_error * nonlin(l1, deriv = TRUE)
	## update weights
  syn1 <- syn1 + 0.01 * t(l1) %*% l2_delta
  syn0 <- syn0 + 0.01 * t(l0) %*% l1_delta
  M[j + 2*iter,2] <- sd(y - l2)
}

M <- data.frame(M)
M <- transform(M, X3 = as.factor(X3))	
names(M) <- c('iter','MSE','Class')
library(ggplot2)
ggplot(data = M, mapping = aes(x = iter, y = MSE, colour = Class)) + 
    geom_line(linewidth = 1.5) + ylim(0,.65)

exp

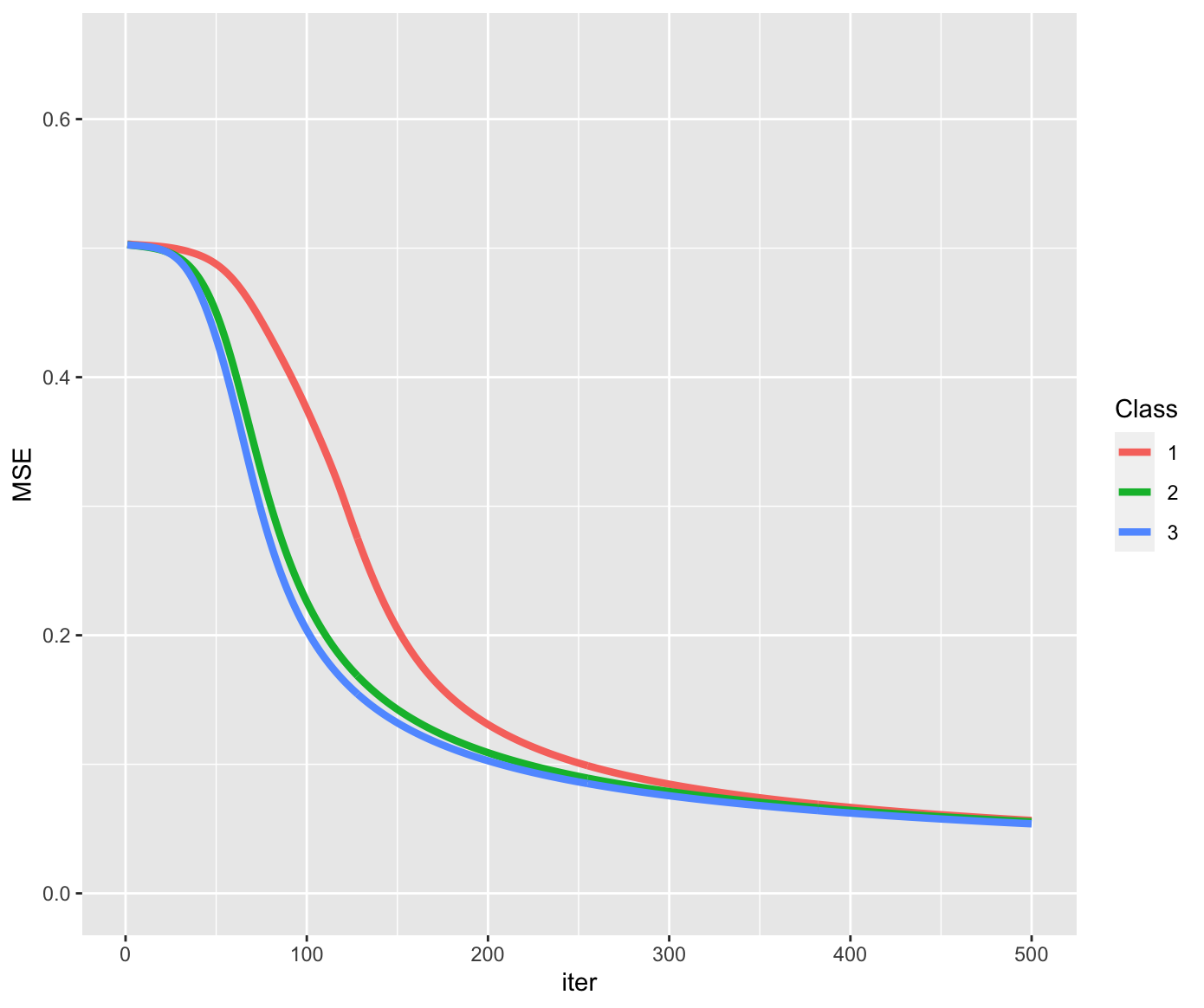
可以看到标准化和中心化都可以更快速的求得结果。