1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
| setwd("D:\\doc\\Mandelbrot\\pic")
jet.colors <-
colorRampPalette(
c(
"#00007F",
"blue",
"#007FFF",
"cyan",
"#7FFF7F",
"yellow",
"#FF7F00",
"red",
"#7F0000"
)
)
m = 400
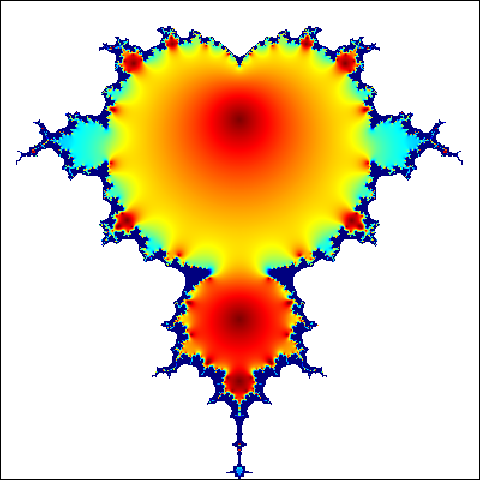
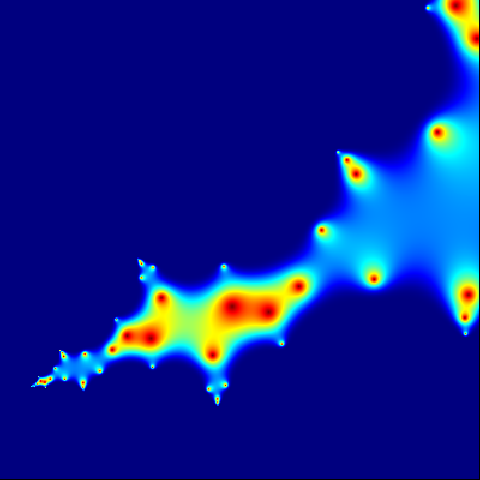
C = complex(real = rep(seq(-1.8, 0.6, length.out = m), each = m),
imag = rep(seq(-1.2, 1.2, length.out = m), each = m))
C = matrix(C, m, m)
Z = 0
for (j in 1:20) {
Z = Z ^ 2 + C
X = exp(-abs(Z))
}
png("scale1.png")
par(mar = c(0, 0, 0, 0))
image(X, col = jet.colors(1000))
dev.off()
m = 400
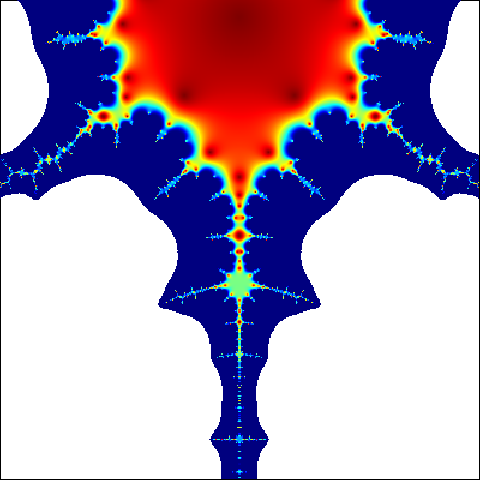
C = complex(real = rep(seq(-1.6, -1.3, length.out = m), each = m),
imag = rep(seq(-0.15, 0.15, length.out = m), m))
C = matrix(C, m, m)
Z = 0
for (j in 1:20) {
Z = Z ^ 2 + C
X = exp(-abs(Z))
}
png("scale2.png")
par(mar = c(0, 0, 0, 0))
image(X, col = jet.colors(1000))
dev.off()
m = 400
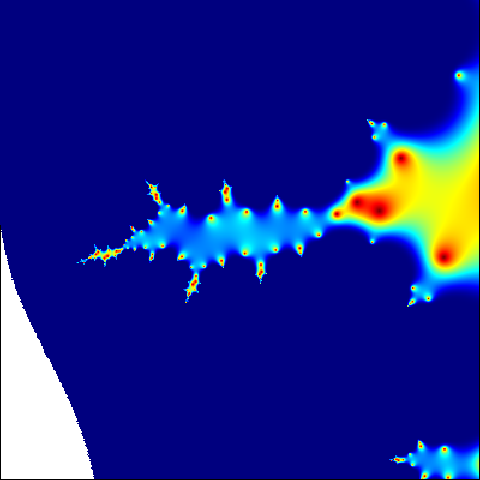
C = complex(real = rep(seq(-1.4, -1.3, length.out = m), each = m),
imag = rep(seq(-0.15, -0.05, length.out = m), m))
C = matrix(C, m, m)
Z = 0
for (j in 1:20) {
Z = Z ^ 2 + C
X = exp(-abs(Z))
}
png("scale3.png")
par(mar = c(0, 0, 0, 0))
image(X, col = jet.colors(1000))
dev.off()
m = 400
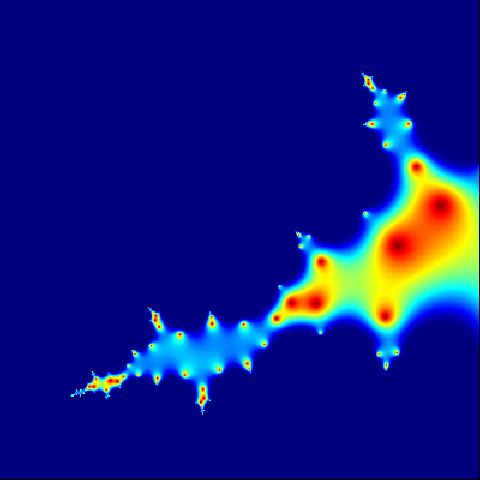
C = complex(real = rep(seq(-1.35, -1.30, length.out = m), each = m),
imag = rep(seq(-0.13, -0.08, length.out = m), m))
C = matrix(C, m, m)
Z = 0
for (j in 1:20) {
Z = Z ^ 2 + C
X = exp(-abs(Z))
}
png("scale4.png")
par(mar = c(0, 0, 0, 0))
image(X, col = jet.colors(1000))
dev.off()
m = 400
C = complex(real = rep(seq(-1.3280, -1.3250, length.out = m), each = m),
imag = rep(seq(-0.1225, -0.1195, length.out = m), m))
C = matrix(C, m, m)
Z = 0
for (j in 1:20) {
Z = Z ^ 2 + C
X = exp(-abs(Z))
}
png("scale5.png")
par(mar = c(0, 0, 0, 0))
image(X, col = jet.colors(1000))
dev.off()
m = 400
C = complex(real = rep(seq(-1.3276, -1.3270, length.out = m), each = m),
imag = rep(seq(-0.1221, -0.1215, length.out = m), m))
C = matrix(C, m, m)
Z = 0
for (j in 1:20) {
Z = Z ^ 2 + C
X = exp(-abs(Z))
}
png("scale6.png")
par(mar = c(0, 0, 0, 0))
image(X, col = jet.colors(1000))
dev.off()
|