合成双重差分法

发表于 2023-05-20 分类于算法

1. 研究背景

1988 年 11 月，California 发起了一项名为”99 号提案“的选民倡议，该提案是美国第一个现代大规模烟草控制项目（次年 1 月正式生效）。在该法案的有两项主要内容：

California 的每包香烟香烟的消费税（cigarette excise tax）提高了 25 美分；
法案的所得收入专项用于控烟的教育与媒体宣传。

P.S. California 香烟消费税现在是每包 87 美分，为美国最高的州之一。

该法案在后续引发了一系列关于室内清洁空气的地方立法。那问题来了：

在 California 该项法案的实施，对烟草控制是积极的还是消极的？影响有多大？

2. 数据情况

美国各州从 1970 年开始有完整的香烟消费的数据，随着健康理念的深入，到 2000 年大部分州也实施了禁烟措施。因此该案例的观察周期是从 1970 年至 2000 年之间。出于研究准确性的考虑，删除了部分州的数据：

期内采用其他一些大规模烟草控制计划的州（马萨诸塞州、亚利桑那州、俄勒冈州和佛罗里达州）
在 1989 至 2000 年期间将州烟税提高 50 美分或更高的州（阿拉斯加、夏威夷、马里兰，密歇根、新泽西、纽约、华盛顿、哥伦比亚特区）

最后样本池中剩下 38 个州，其他字包含了年份（Year），人均消费卷烟数（PacksPerCapita）。数据大概长这个样子：

State	Year	PacksPerCapita
Alabama	1970	89.8
Arkansas	1970	100.3
Colorado	1970	124.8
Connecticut	1970	120.0
...	...	...
West Virginia	2000	107.9
Wisconsin	2000	80.1
Wyoming	2000	90.5
California	2000	41.6

先用最简化的思路来看 99 法案是否有效。

3. 双重差分 (DID)

双重差分（difference in differences）是一种常见的计量经济学方法，用于评估政策或干预措施的影响。它的基本思想是对比实验组和对照组在政策实施前后的差异，以确定政策的影响。

California 控烟的这个案例中，DID 方法可以通过以下步骤进行：

确定实验组（加州）和对照组（其他州）；
确定政策实施的时间节点（1970-1988 vs 1989-2000）；
对比政策实施前后实验组和对照组之间的差异（第 1 次差异）；
对比政策实施前后实验组内部和对照组内部之间的差异（第 2 次差异）；
比较第 3 步和第 4 步的差异（所以叫做双重差分），以确定政策的影响。

DID 方法的优点是可以控制时间不变的因素，从而更准确地评估政策的影响。以上思想我们落在实际数据上：

	时间段	人均消费卷烟数
加州	1970-1988	116.2
加州	1989-2000	60.3
其他州	1970-1988	130.6
其他州	1989-2000	102.1

结论是：加州从 116.2 下降到 60.3，其他州从 130.6 下降到 102.1。加州的"对比降幅"是要高于其他州的，因此这项政策是有效果的。

4. 合成双重差分 SDID 是什么？

Synthetic difference in differences (SDID)是一种利用合成控制组的方法来评估政策干预效果的分析技术。其基本原理是将政策实施地区的观测结果与一个合成控制组进行比较，以便更准确地衡量政策效果。

SDID 方法的基本步骤如下：

选择一个与政策实施地区在政策实施前相似的合成控制组
使用控制组的数据建立预测模型来估计政策实施地区在政策实施前的预期结果
然后比较政策实施地区的观测结果与合成控制组的预测结果，以便评估政策干预效果。

SDID方法可以更准确地评估政策干预效果，因为它可以控制其他可能影响结果的因素，并且可以更好地匹配政策实施地区和合成控制组的特征。

以下是部分城市和部分年份的示例：

Year	Alabama	Arkansas	Colorado	Connecticut	Delaware	Georgia	Idaho
1970	89.8	100.3	124.8	120.0	155.0	109.9	102.4
1971	95.4	104.1	125.5	117.6	161.1	115.7	108.5
1972	101.1	103.9	134.3	110.8	156.3	117.0	126.1
1973	102.9	108.0	137.9	109.3	154.7	119.8	121.8
1974	108.2	109.7	132.8	112.4	151.3	123.7	125.6
1975	111.7	114.8	131.0	110.2	147.6	122.9	123.3

我们需要构建一个 1989 年之后没有受到 99 法案影响的 California，有一个非常容易想到的思路就是使用 1989 年之前的其他城市对 California 进行拟合，求出来的模型应用在 1989 年之后，即获得了一个的合成 California

首先看一下拟合出来的模型什么样？

	系数
(Intercept)	6.59
Colorado	0.05
Connecticut	0.17
Idaho	0.04
Illinois	0.16
Montana	0.14
Nebraska	0.14
Nevada	0.17
New Hampshire	0.01
Tennessee	-0.24
Utah	0.22
West Virginia	0.07

也就是说 California 的人均消费卷烟数可以这样表示：

\[ C_{California} = 6.59 + 0.05C_{Colorado} + 0.17C_{Connecticut} + 0.04C_{Idaho} + \cdots + 0.07C_{West Virginia} \]

这个公式合成了一个实际上并不存在的 California，我们假设

其他州在后续的时间没有大规模的变化；
1988 年之前 California 可以被其他州的线性组合替代，1989 年之后线性关系依然存在。

这样我们就可以通过真实发生的 California 数据，对比这个合成 California 数据，来观察政策带来的影响：

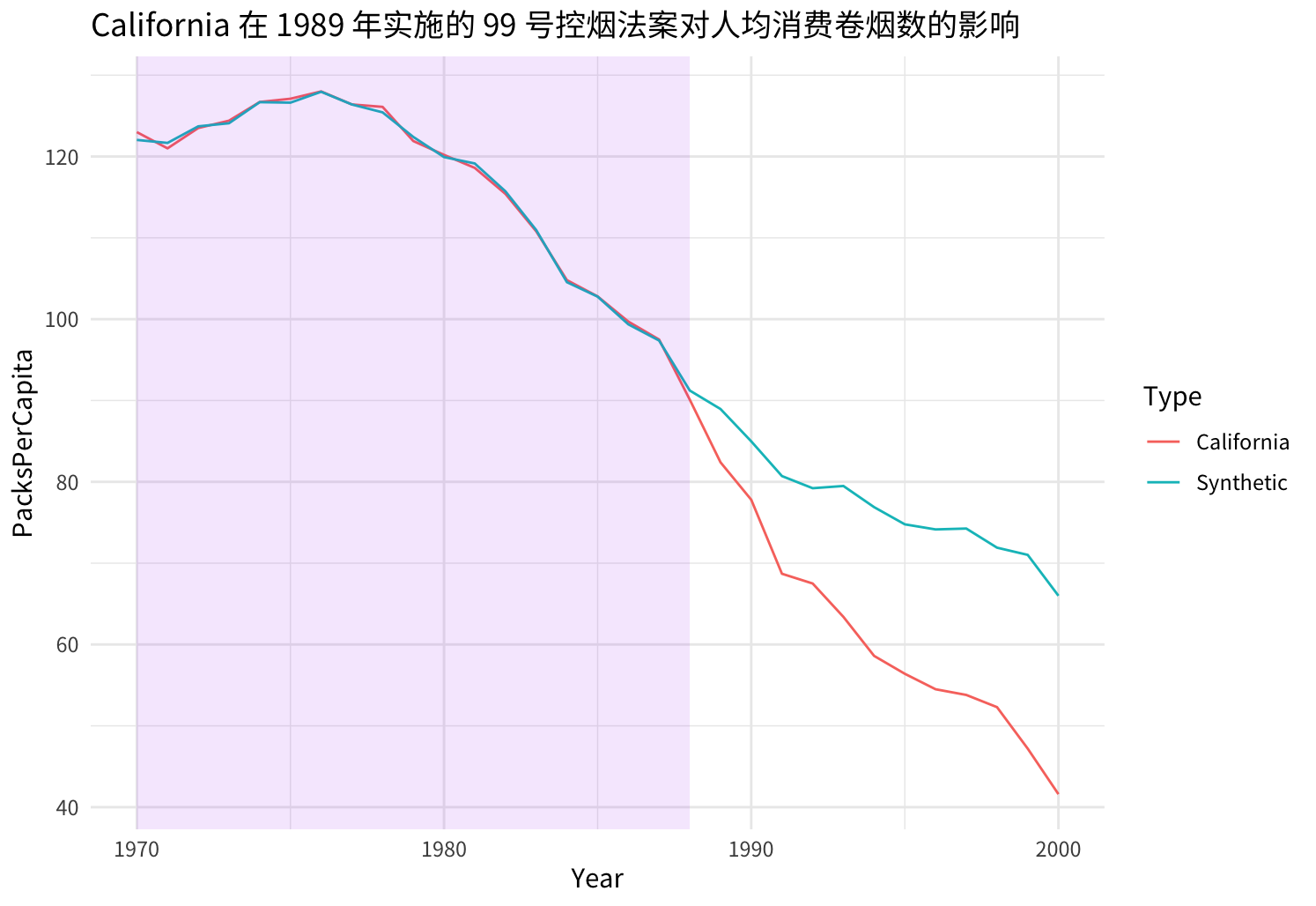
根据以上构建的合成双重差分法得到的分析结果看，加州实施的烟草控制计划的影响就非常显然了。在第 99 号提案之后：

California 每年的人均消费卷烟数逐年下降，且呈现扩大趋势；
在 2000 年，California 年人均消费卷烟数比没有第 99 号提案时的情况低了约 24 包。

5. 其他问题的讨论

该方法很容易将线性模型升级为非线性模型，从笔者的实际业务操作上看，该方法的稳健性和解释性可以到大幅提升。

6. 附数据和代码

#| message: false
## DID 部分
library(tidyverse)
library(knitr)
library(ggplot2)
prop99_tr <- read.csv('https://bjt.name/upload/csv/california_prop99.csv')
prop99_tr$treated[prop99_tr$Year >= 1989] <- '1989-2000'
prop99_tr$treated[prop99_tr$Year < 1989] <- '1970-1988'
s_prop99_tr <- prop99_tr |> 
  group_by(State, treated) |>
  summarise(ave = mean(PacksPerCapita), .groups = 'keep')
s_prop99_tr |> mutate(
  New_class = ifelse(State == 'California', 'california', 'else')
) |>
  group_by(New_class, treated) |>
  summarise(v = mean(ave), .groups = 'keep') |>
  kable()

data_wide_all <- prop99_tr |> pivot_wider(
    id_cols = "Year", 
    names_from = "State", 
    values_from = "PacksPerCapita"
  )

## 拟合 SDID 的线性模型
data_wide <- subset(data_wide_all, Year < 1989)
library(glmnet)
Y = data_wide$California
X = select(data_wide,-c('Year', 'California')) |> as.matrix()
model_glmnet <- cv.glmnet(y = Y, x = X , family = 'gaussian')
# model_glmnet
coef(model_glmnet, s = "lambda.min") |> round(2)

X_all <-
  select(data_wide_all,-c('Year', 'California')) |> as.matrix()
DID_data <- data.frame(
  Year = data_wide_all$Year,
  California = data_wide_all$California,
  Synthetic = predict(
    model_glmnet, newx = X_all, s = 0.1089)[,1]
) |> gather('Type', 'PacksPerCapita', -Year)

## 绘制差异图
gs <- tribble(
  ~start, ~end,
  1970, 1988,
)
ggplot(data = DID_data, aes(x = Year, y = PacksPerCapita, colour = Type)) +
  geom_line() +
  geom_rect(
    data = gs,
    aes(
      xmin = start,
      xmax = end,
      ymin = -Inf,
      ymax = Inf
    ),
    fill = 'purple',
    alpha = 0.1,
    show.legend = FALSE,
    inherit.aes = FALSE
  ) +
   labs(title = 'California 在 1989 年实施的 99 号控烟法案对人均消费卷烟数的影响') +
    theme_minimal(base_family = 'Noto Sans SC')