合成控制法的原理和扩展实现
1. 案例场景
假设你是肯德基的门店运营负责人,某天,你们决定在某家分店(称为 A 店)推出买一送一的促销活动。你想评估这项促销活动的效果,看看它是否提高了这家分店的销售额。
这个评价问题在于,你只有一家分店进行了促销活动,其他的分店都没有进行相同的促销。你无法直接比较 A 店的销售额和没有进行促销的分店的销售额,因为这些分店可能本身就存在很多差异,比如地理位置、人流量等因素。
但通过使用其他分店(控制组)的数据来构建一个“虚拟”的对照组,这个虚拟的对照组在没有促销的情况下表现得和 A 店相似。通过比较促销之后实际的 A 店和这个虚拟对照组的业绩,就可以评估促销活动的效果。
- 收集 A 店在促销活动前后的一段时间内的销售数据。
- 收集其他分店在同一时间段内的销售数据。
- 选择一些影响销售额的关键特征,比如每天的顾客数量、人均消费额等。
通过对其他分店的特征进行加权平均,构建一个“合成”分店,使其在促销活动开始之前的特征与 A 店尽可能相似。例如,假设你选择了三家分店 B、C 和 D,它们在促销开始前的特征分别是:
- B 店:顾客数量 100 人,人均消费额 20 元;
- C 店:顾客数量 150 人,人均消费额 25 元;
- D 店:顾客数量 200 人,人均消费额 30 元。
如果你发现 A 店在促销开始前的特征是顾客数量 150 人,人均消费额 25 元,那么你可以给 B、C、D 店分配权重,使得加权平均后的特征与 A 店相近。比如,权重可能是 B 店 20%,C 店 60%,D 店 20%。
实际和合成控制组有这样的比较效果:
- 促销活动前 A 店销售额序列和合成组(由其他分店加权平均得到)销售额序列基本一致。
- 活动后,比较 A 店的实际销售额与合成控制组的预测销售额。
- 如果 A 店的实际销售额显著高于合成控制组的预测销售额,那么可以认为促销活动是有效的。
以上是一个简单的原理说明,下面从详细的数学理论做完整推导和扩展。
2. 数学原理
以上方法被称为合成控制法(Synthetic Control Method, 简称 SCM),它是一种用于评估政策干预效果的统计方法,特别适用于只有一个或少数几个单位接受了干预的情况。这种方法通过构建一个“合成控制”组来模拟未接受干预的单位,从而估计干预的效果。
假设我们有 \(J+1\) 个单元,其中第 1 个单元是处理单元,其余 \(J\) 个单元是对照单元。我们观测到每个单元在 \(T\) 个时间段内的结果变量 \(Y\) 和协变量 \(X\)。
对于协变量 \(X_i\),我们可以定义一个权重矩阵 \(V\) 来反映不同协变量向量的重要性。假设 \(X_i\) 包含了 \(k\) 个向量。\(i\) 是列,\(k\) 是行,则 \(V\) 可以是一个 \(k \times k\) 的对角矩阵,其中对角线上的元素代表每个(行)向量的相对重要性。
定义:
- \(Y_{it}\):单元 \(i\) 在时间 \(t\) 的结果变量。
- \(X_{i}\):单元 \(i\) 的协变量。
- \(V_{k \times k}\):\(X_{i}\) 中 \(k\) 个向量的权重。
换一个经典的美国加州控烟效果的数据集来说明,\(X_i\) 的示例数据如下:
| Tennessee | Georgia | Texas | Utah | |
|---|---|---|---|---|
| lnincome | 0.157 | 0.157 | 0.162 | 0.165 |
| beer | 0.126 | 0.123 | 0.167 | 0.138 |
| age15to24 | 0.161 | 0.152 | 0.165 | 0.150 |
| retprice | 0.166 | 0.167 | 0.149 | 0.191 |
| cigsale1975 | 0.126 | 0.130 | 0.148 | 0.125 |
| cigsale1980 | 0.140 | 0.150 | 0.149 | 0.134 |
| cigsale1988 | 0.155 | 0.168 | 0.131 | 0.145 |
\(X_i\) 的列向量则是美国各个州的表现,行向量有 7 个,分别对应的是
- 在 1970 年至 1988 年之间的平均数:收入的对数(lnicome)、消费的啤酒量(beer)、15 至 24 岁的人口比例、香烟售卖均价。
- 以及重点关注的 1975、1980、1988 年香烟售卖量。
这里需要注意的一点是,由于研究目的或者数据记录缺失等问题,\(X_i\) 很可能不是一个面板数据。
\(Y_{jt}\) 表示的是各个州在 1970 至 2000 年之间的每年香烟消费量,这是我们最关注部分。示例数据如下:
| year | Alabama | Arkansas | Colorado | Connecticut | Delaware |
|---|---|---|---|---|---|
| 1970 | 89.8 | 100.3 | 124.8 | 120.0 | 155.0 |
| 1971 | 95.4 | 104.1 | 125.5 | 117.6 | 161.1 |
| 1972 | 101.1 | 103.9 | 134.3 | 110.8 | 156.3 |
| 1973 | 102.9 | 108.0 | 137.9 | 109.3 | 154.7 |
| 1974 | 108.2 | 109.7 | 132.8 | 112.4 | 151.3 |
| 1975 | 111.7 | 114.8 | 131.0 | 110.2 | 147.6 |
| 1976 | 116.2 | 119.1 | 134.2 | 113.4 | 153.0 |
| ... | ... | ... | ... | ... | ... |
合成控制组的构建:
选择一组权重 \(\mathbf{w} = (w_2, w_3, \ldots, w_{J+1})\),使得 \(\sum_{j=2}^{J+1} w_j = 1\) 且 \(w_j \geq 0\)。
构建合成控制组的协变量向量 \(\hat{X}_1\):
\[ \hat{X}_1 = \sum_{j=2}^{J+1} w_j X_j \]
构建合成控制组的结果变量 \(\hat{Y}_{1t}\):
\[ \hat{Y}_{1t} = \sum_{j=2}^{J+1} w_j Y_{jt} \]
这时候我们拥有两个损失(在处理前的时间段 \(T\) 内):
\[LOSS^Y = \sum_{t=1}^{T} \left( Y_{1t} - \sum_{j=2}^{J+1} w_j Y_{jt} \right)^2\]
\[LOSS^X = (X_1 - \sum_{j=2}^{J+1} w_j X_j)' V (X_1 - \sum_{j=2}^{J+1} w_j X_j)\]
如果有一个 \(\mathbf{w}\) 能够使得 \(LOSS^Y, LOSS^X\) 都能够最小化。这样我们就找到了一个合成州,它的协变量、结果变量均和处理单元表现的非常接近。那么,单元在处理后的因果效应 \(\tau_{1t}\) 定义为处理单元和合成控制组在处理后的结果变量之差:
\[ \tau_{1t} = Y_{1t} - \hat{Y}_{1t} \]
注意,这里 \(Y_i\) 的行向量权重被认定为 1,因为它们是同样属性的内容,都是香烟的年消费量,权重相等。但 \(X_i\) 的行向量属性不同,它们有些是处理前时间内的汇总数据,有些则是具体某年的 \(Y_i\)(业务表达为起始初始值相同)。这些因素对 \(Y_i\) 的解释性也不同,因此权重阵 \(V\) 被考虑了。这也合成控制法的核心思想之一。
在实际应用中,协变量 \(X_i\) 通常包括一些在处理前已知的、与结果变量相关的特征。通过将这些协变量纳入合成控制组的构建过程中,可以提高合成控制组的合理程度,从而更准确地估计因果效应。
3. 嵌套最优化
前文描述是一个非常粗略的解释,合成控制法的的实际优化目标是:
\[\min_{V} \left(Z_1 - Z_0 W^{(V)}\right)^{T} \left(Z_1 - Z_0 W^{(V)}\right)\]
- \(V\) 是 \(k\) 个协变量向量的权重。
- \(W^{(V)}\) 是合成控制组(\(J\) 个对照单元)的权重向量,基于 \(X_1\) 和 \(X_0\) 求解。\(X_1\) 和 \(X_0\) 分别是,处理组协变量和 \(J\) 个对照组协变量。
- \(Z_1\) 和 \(Z_0\) 分别是,在处理时间段 \(T\) 内,处理组结果变量和 \(J\) 个对照组结果变量。
\(V\) 和 \(W\) 是需要优化两个参数。
请注意,合成控制法是本质是用 \(V\) 找合成结果变量,最小化 \(LOSS^{Y}\)。\(W\) 只是顺道求解出来的中间结果,\(W\) 并不被直接求解。
这问题的解法稍有一点绕,涉及到嵌套最优化:我们需要先优化一个目标函数,然后将优化结果用于另一个目标函数的优化。具体来说,可以分解为以下两个步骤:
- 优化 \(W\) 使得 \(\left|X_1 - X_0 W\right|_V\) 最小化。
- 使用前一步得到的 \(W\) 来优化 \(V\) 使得 \(\left(Z_1 - Z_0 W^{(V)}\right)^{T} \left(Z_1 - Z_0 W^{(V)}\right)\) 最小化。
3.1. 第一步:优化 \(W\)
首先,我们需要最小化 \(\left|X_1 - X_0 W\right|_V\),即:
\[\left|X_1 - X_0 W\right|_V^2 = \left(X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W\right)\]
可以通过求解以下方程来找到 \(W\):
\[\min_W \left(X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W\right) = \min_W (X_1^T V X_1 - 2 X_1^T V X_0 W + W^T X_0^T V X_0 W)\]
设 \(A = X_0^{T} V X_0\) 和 \(B = X_0^{T} V X_1\),则问题变为:
\[\min_W (X_1^{T} V X_1 - 2 B^{T} W + W^{T} A W)\]
对 \(W\) 求导并令其等于零。
由于 \(X_1^{T} V X_1\) 不依赖于 \(W\),因此求导过程等价于:
\[ \frac{\partial}{\partial W} (-2 B^{T} W + W^{T} A W) = -2 B + 2 A W = 0 \]
得到:
\[2 A W - 2 B = 0\] \[A W = B\] \[W = A^{-1} B\]
但这个方法有个弊端,一旦 \(A\) 是奇异矩阵(singular matrix),则 \(A^{-1}\)无解。所以需要转化一下思路。同上文描述,由于 \(X_1^T V X_1\) 不依赖于 \(W\),因此
\[\min_W \left(X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W\right)\]
等价于
\[\min_W (W^T X_0^T V X_0 W - 2 X_1^T V X_0 W)\]
假如我们设:
- \(H = X_0^T V X_0\)
- \(c = -2 X_1^T V X_0\)
是一个二次规划问题:
\[w^T H w + c^T w\]
同时考虑到 \(w\) 限制条件,即
\[ \begin{align*} & \text{minimize} && \mathbf{w}^T H \mathbf{w} + c^T \mathbf{w} \\ & \text{subject to} && \mathbf{w} \geq 0 \\ & && \sum_{j=2}^{J+1} w_j = 1 \end{align*} \]
\(X_0\) 和 \(X_1\) 是常数阵,任意给定 \(V\),都可以求得符合条件的 \(W\),使得 \(\left|X_1 - X_0 W\right|_V^2\) 最小。
3.2. 第二步:优化 \(V\)
使用第一步中优化得到的 \(W\),接着最小化:
\[\left(Z_1 - Z_0 W^{(V)}\right)^{T} \left(Z_1 - Z_0 W^{(V)}\right)\]
想象一下,\(W^{(V)}\) 是 \(V\) 的函数,任意个 \(V\) 就可以得到 \(W\),并计算出上式的 loss,所以这是一个关于 \(V\) 的优化问题(嵌套了一层 \(W\))。我们需要找到 \(V\) 使得上述表达式最小化。
到这一步就容易了,可以借助通用梯度下降法来求解。合成控制法的这两个步骤很巧妙,通过嵌套的方式同时保证了 \(Loss^Y, Loss^X\) 均为最小。
当然,将最优的 \(V\) 求解出来后,还需要重新执行一遍第一步,以获得最优 \(W\)。
3.3. 系数和模型表现
使用前述方式计算各个参数,\(V\) 的结果为:
1 | v.names v |
\(W\) 的结果为:
1 | state_name w |
合成的 \(\hat{Y}_{1t}\) 同原始 \(Y_{1t}\) 的对比曲线如下图所示:
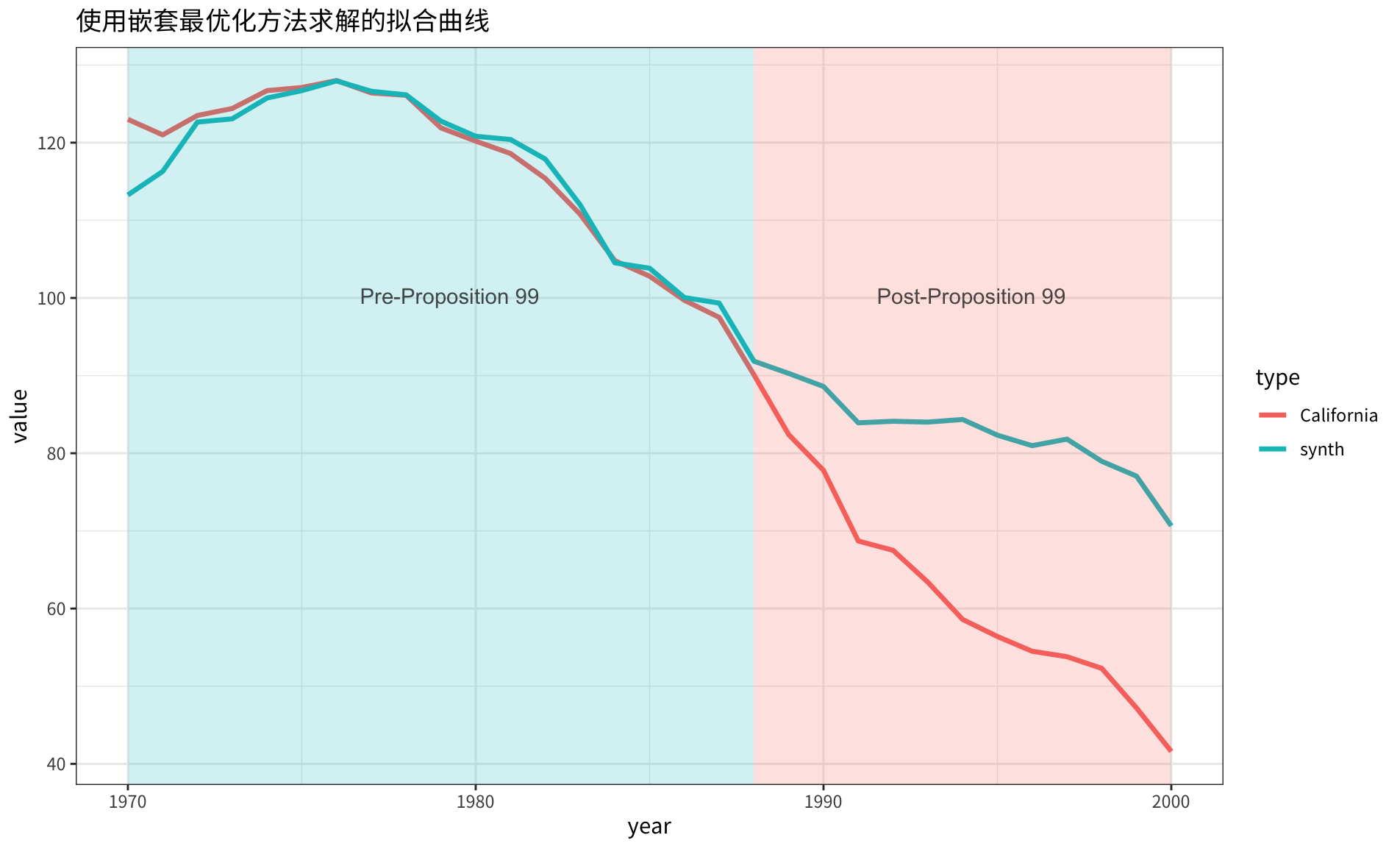
4. 重定义损失函数
合成控制法通过嵌套最优化的方法,得到两个参数 \(W, V\) 的最优值。但实际上,大家仔细想想:难道我们不清楚协变量中各个向量的重要性吗?用模型算一个最优的 \(V\) 你敢直接用吗?业务解释性如何?
我们可否用一个更加通用的损失函数,能够同时考虑结果变量和协变量?答案显然是可以的!一旦通过某种手段求解了 \(V\),简单的将 \(LOSS^X\) 和 \(LOSS^Y\) 加起来就是解法之一。下面我们看看这个方法的可行性和效果。
首先是协变量的权重 \(V\) 的求解,有几种思路可供参考:
- 基于先验业务,为每个协变量赋予一个权重,比如 AHP 专家评分法。
- 如果 \(X_i\) 同 \(Y_i\) 一样是面板数据,那么基于机器学习算法,估计 \(X_i\) 各个向量的对 \(Y_i\) 的影响,影响权重即为协变量的重要性。
4.1. 机器学习估计 \(V\)
从数据出发,什么因素会影响到各州的香烟消费量?\(X_i\) 中 4 个要素:收入的对数(lnicome)、消费的啤酒量(beer)、15 至 24 岁的人口比例(age15to24)、香烟售卖均价(retprice)。当然,各州的本身,它们也是影响香烟消费量的关键因素。
数据可以构建这样(各州本身被转换为了 0,1 特征):
| id | cigsale | lnincome | beer | age15to24 | retprice | Alabama | Georgia | Kentucky | New Mexico | Texas |
|---|---|---|---|---|---|---|---|---|---|---|
| 149 | 122.8 | 9.769 | 23.629 | 0.162 | 51.5 | 0 | 0 | 1 | 0 | 0 |
| 756 | 107.0 | 9.894 | 32.100 | 0.169 | 106.8 | 0 | 0 | 0 | 0 | 0 |
| 684 | 146.8 | 9.699 | 23.629 | 0.185 | 39.8 | 0 | 0 | 0 | 1 | 0 |
| 3 | 101.1 | 9.498 | 23.629 | 0.181 | 42.3 | 1 | 0 | 0 | 0 | 0 |
| 134 | 128.6 | 9.756 | 23.629 | 0.181 | 78.9 | 0 | 1 | 0 | 0 | 0 |
| 130 | 131.0 | 9.729 | 23.629 | 0.191 | 56.6 | 0 | 1 | 0 | 0 | 0 |
| 673 | 73.6 | 9.628 | 23.629 | 0.195 | 68.1 | 0 | 0 | 0 | 0 | 1 |
| 583 | 118.7 | 9.509 | 23.629 | 0.201 | 34.1 | 0 | 0 | 0 | 0 | 0 |
| 246 | 223.0 | 9.579 | 23.629 | 0.186 | 33.3 | 0 | 0 | 1 | 0 | 0 |
各位看官看到这里,应该有感觉了,有太多机器学习方法可以获得每个特征的重要性。比如通过随机森林找到各个特征的重要程度,去除州的影响之后,测算得到 \(V\) 为:
| lnincome | beer | age15to24 | retprice |
|---|---|---|---|
| 0.17 | 0.16 | 0.31 | 0.36 |
这个权重同我们的常识相对一致:刨除州本身的影响后,最大影响因素依次是香烟价格、15-24 岁人口、收入的对数、啤酒销量。需要注意的是,这种求解方法只适应于协变量 \(X_i\) 是面板数据,像原始论文那样,把 1975、1980、1988 年的香烟销售量同样作为协变量,这个方法不适用。
4.2. 合并损失函数
只要 \(V\) 就绪,就可以优化以下损失函数以求解 \(w\)。这个损失函数由 \(LOSS^X\) 和 \(LOSS^Y\) 合并而得。
\[ \min_{\mathbf{w}} \left( \lambda (Z_1 - Z_0 W)^{T}(Z_1 - Z_0 W) + (X_1 - X_0 W\right)^{T} V \left(X_1 - X_0 W) \right) \]
其中,\(\lambda\) 是一个权重,用于平衡结果变量和协变量的拟合程度。是更倾向于结果变量一致,还是协变量。
注意:为了保证 \(\lambda\) 权重有效,结果变量和协变量需要归一化,比如这里利用的是“单位向量归一化”方法:
\[ \text{normalized}(x_i) = \frac{x_i}{\sqrt{\sum_{j=1}^{n} x_j^2}} \]
4.3. 系数和模型表现
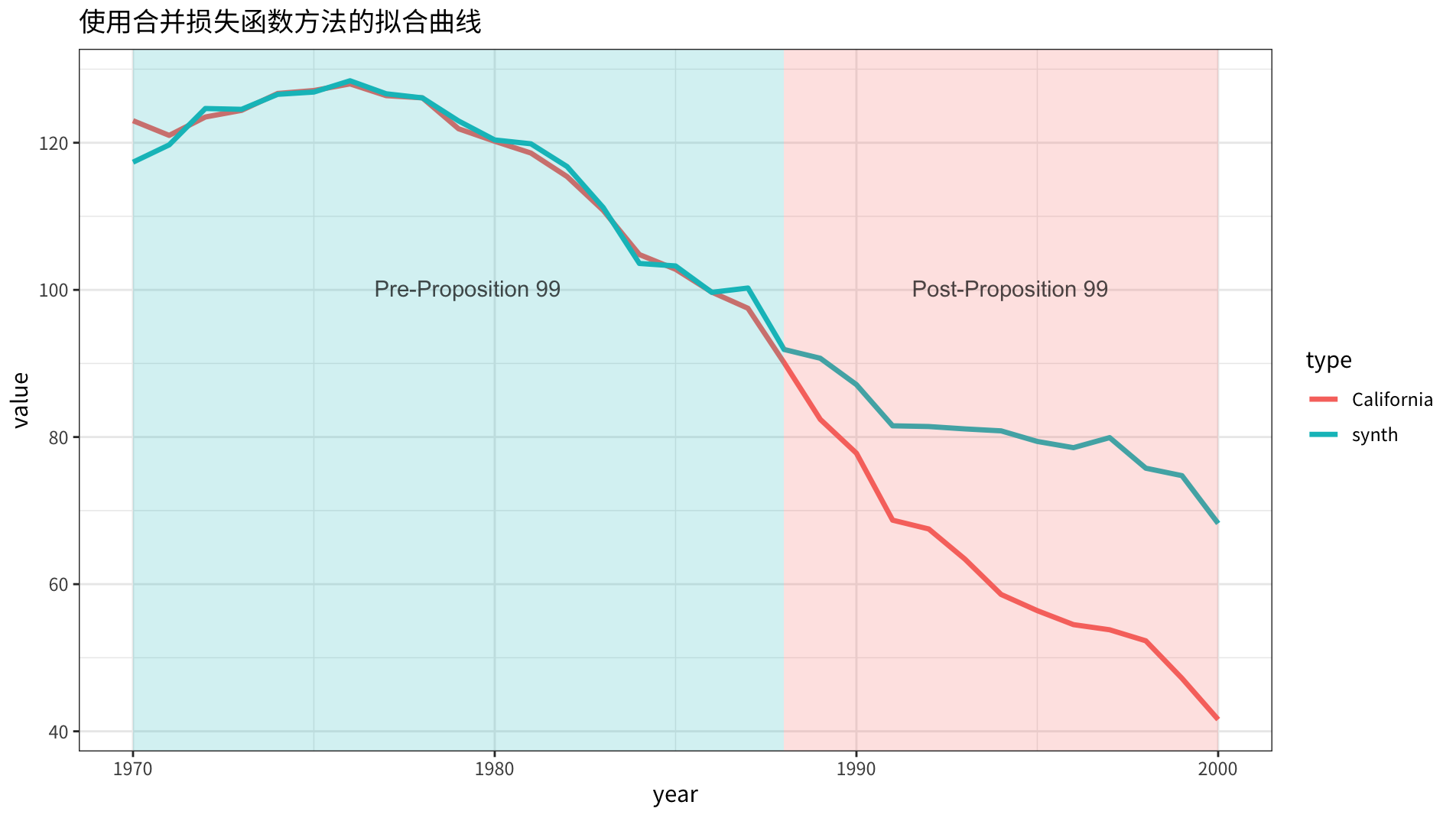
\(\lambda = 1\) 时,结果变量和协变量拟合程度的权重相等。
在 \(V\) 的权重控制下,后两项的相似程度更接近,对业务解释显然更加友好。
| syth_data | X1_meta | diff(%) | |
|---|---|---|---|
| lnincome | 9.818 | 10.032 | 0.021 |
| beer | 23.735 | 24.280 | 0.022 |
| age15to24 | 0.180 | 0.179 | 0.010 |
| retprice | 65.889 | 66.637 | 0.011 |
而且 \(W\) 的不为 0 的数量居然还更少(合成州数量少)!
1 | name w |
合成的 \(\hat{Y}_{1t}\) 同原始 \(Y_{1t}\) 的对比曲线如下图所示:
\(\lambda = 0.01\) 时,这个结果更倾向于协变量的拟合,可以看到:合成的协变量向量,除 lnincome 外,几乎完全一致。
| syth_data | X1_meta | diff(%) | |
|---|---|---|---|
| lnincome | 9.839 | 10.032 | 0.019 |
| beer | 24.312 | 24.280 | 0.001 |
| age15to24 | 0.179 | 0.179 | 0.002 |
| retprice | 66.634 | 66.637 | 0.000 |
合成的 \(\hat{Y}_{1t}\) 同原始 \(Y_{1t}\) 的对比曲线如下图所示:
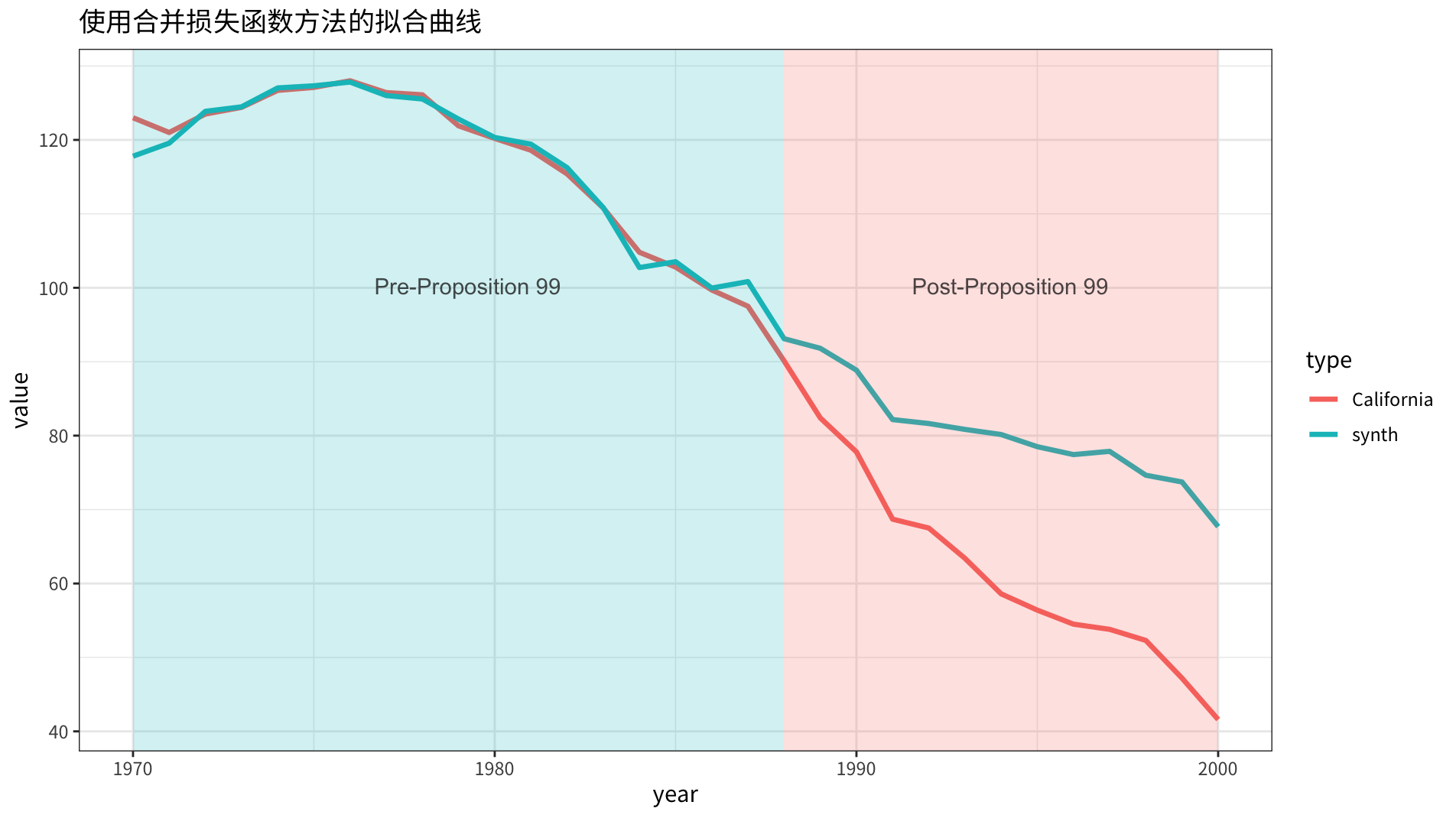
从结果变量的拟合结果上看,两者有细微的差别。因为权重低,整体表现要比 \(\lambda=1\) 时要差一些。
5. 同时做变量选择
设想以下需求场景:
- 假如观测的段 \(T\) 为 20,但是对照单元 \(J\) 为 1000,那么合成控制组的构建会变得非常困难。在这种情况下,我们需要尽可能压缩权重向量 \(w\),以简化合成控制组的构建。
- 前文提到的方法是最小化 \(Z_1 - Z_0 W\) 的平方误差,但如果模型过拟合怎么办?泛化能力过弱怎么办?
当然,这个想法是有代价的,不可能既要又要还要。这时需要酌情放宽 \(w\) 的限制条件,不再要求 \(\sum_{j=2}^{J+1} w_j = 1\) 且 \(w_j \geq 0\) 这两个条件。
5.1. 具体实现过程
在合成控制法中,我们更关注的是结果变量 \(Y\) 的拟合,而协变量 \(X\) 主要用于辅助构建合成控制组。通过权重 \(\lambda, V\) 将 \(Y\) 和 \(X\) 合并成为一个统一的响应变量,并使用权重向量 \(\mathbf{w}\) 来构建合成控制组。
假设我们有 \(J+1\) 个单元,其中第 1 个单元是处理单元,其余 \(J\) 个单元是对照单元。我们观测到每个单元在 \(T\) 个时间段内的结果变量 \(Y\) 和协变量 \(X\)。
定义:
- \(Y_{it}\):单元 \(i\) 在时间 \(t\) 的结果变量。
- \(X_{i}\):单元 \(i\) 的协变量向量。
- \(\lambda\) 正则化参数,用于平衡结果变量和协变量的拟合程度。
- \(V\) 协变量的权重矩阵,用于调整协变量的重要性。
可以将 \(Y\) 和 \(X\) 视为一个扩展的响应变量向量 \(\mathbf{z}_{it}\),其中 \(\mathbf{z}_{it}\) 包含 \(Y_{it}\) 和 \(X_{i}\),表示为:
\[ \mathbf{z}_{it} = \begin{bmatrix} Y_{it} \\ \lambda X_{i} V \end{bmatrix} \]
然后,我们可以定义一个新的目标函数,将 \(Y\) 和 \(X\) 合并在一起:
\[ \min_{\mathbf{w}} \left( \frac{1}{T} \sum_{t=1}^{T} \left( \mathbf{z}_{1t} - \sum_{j=2}^{J+1} w_j \mathbf{z}_{jt} \right)^2 + \alpha \sum_{j=2}^{J+1} |w_j| \right) \]
其中,\(\mathbf{z}_{1t}\) 是处理单元在时间 \(t\) 的扩展响应变量,\(\mathbf{z}_{jt}\) 是对照单元 \(j\) 在时间 \(t\) 的扩展响应变量。
这个目标函数包含两个部分:
- 扩展响应变量的平方误差项。
- L1 正则化项。
这种方式将 \(Y\) 和 \(X\) 合并在一起,并使用类似 LASSO 的方法来求解权重 \(\mathbf{w}\)。在这个框架下,我们就可以采用交叉验证的方法来选择 MSE 效果最好的参数来构建模型,也可以更灵活地处理结果变量和协变量的关系,同时进行变量选择和系数收缩。
5.2. 转化为弹性网络问题
也可以将它改写成 Elastic Net 模型形式:
\[ \min_{\mathbf{w}} \left\{ \frac{1}{T} \sum_{t=1}^{T} \left( \mathbf{z}_{1t} - \sum_{j=2}^{J+1} w_j \mathbf{z}_{jt} \right)^2 + \lambda \left( (1-\alpha)\frac{1}{2}\sum_{j=2}^{J+1}w_j^2 + \alpha \sum_{j=2}^{J+1}|w_{j}| \right) \right\} \]
其中的超参数 \(\alpha\) 和 \(\lambda\) 通过交叉验证的机器学习框架,求解泛化能力最好,且能让 loss 最小的 \(w\)。
5.3. 系数和模型结果
需要注意的是,这种方法很灵活,不需要协变量为面板数据。
1 | X_synth X1 |
合成的 \(\hat{Y}_{1t}\) 同原始 \(Y_{1t}\) 的对比曲线如下图所示:
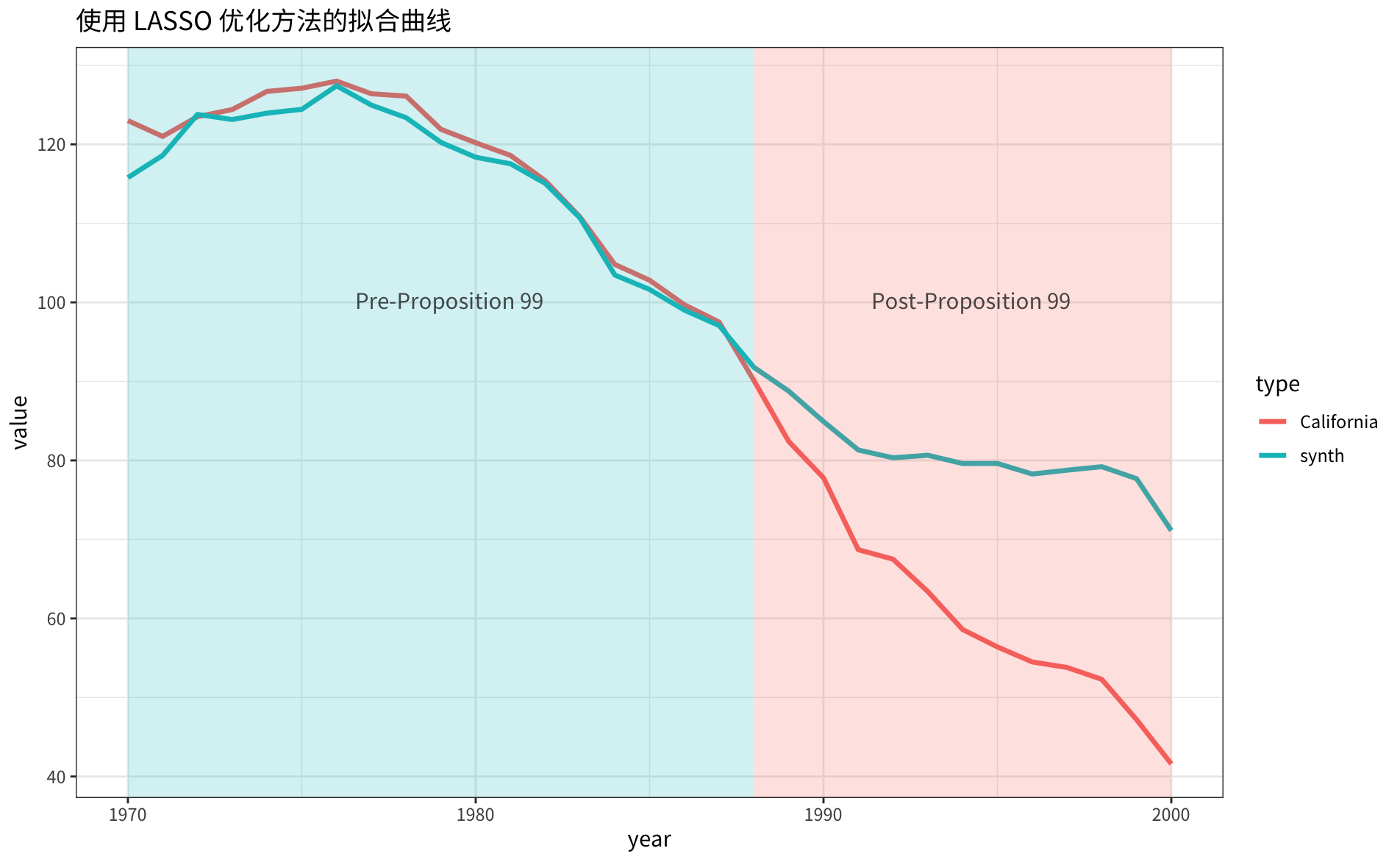
虽然从拟合曲线上比前面的两种方法表现都要差,但我个人还是更加认可这个方法,毕竟通过交叉验证的参数,泛化性更好,结果更加稳健。
当然如果你只关注结果变量 \(Y_i\) 的拟合程度,而不想考虑协变量 \(X_i\) 的影响。恭喜你,你发现了一种新的方法——SDID。
6. 总结
本文注意力主要集中在如何更便捷的求解合成控制法中的参数,并没有更多的讨论安慰剂检验等其他细节。合成控制法是一个非常好的,用于估计政策或活动影响变化的框架。算法细节上使用嵌套优化的方法,非常优雅。但它也有一定局限性,有改进的可能:
- 使用嵌套完全最优化的方法可能会出现过拟合的情况,模型存在稳定性问题,不利于估计因果效用。
- 合并损失的方式是可行方法之一,可以控制输出变量和协变量的权重。但需要留意,\(X\) 和 \(Y\) 都要做归一化处理。
- 引入全新的损失函数,增加正则项,借助通用机器学习框架,可以解决权重 \(w\) 维度过高,以及提升模型的稳健性。
注:三个方法实现的 R 代码 1000 多行,太长,先不贴到原文了。